@ Article: ICML from Microsoft & Huazhong Keda @ Code: Github @ Noteby: Aikenhong @ Time: 20210914

Abstrast and Intro

in the session we will using describe the main idea of this article.

这篇文章的重点在于Soft Teacher，也就是用pseudo label做为弱标注，逐步提高伪标签的可靠性。

不同于多阶段的方法，端到端的方法再训练中逐步的提升伪标签的质量从而再去benifit目标检测的质量。 这样E2E的框架主要依赖于两部分技术:

  • soft teacher: 每个未标记边界框的分类损失由教师网络产生的分类分数进行加权
  • box jitter 窗口抖动: 选择可靠的伪框来学习框回归

在目标检测上获得SOTA的效果;

Multi-Stage

在半监督的情况下，关注的主要是基于伪标签的方法，是目前的SOTA，以往的方法采用多阶段的方式。

  1. 使用标记数据训练初始检测器
  2. 未标记数据的伪标记，同时基于伪标签进行重新训练

局限：初始少量标注的局限，初始的检测器的伪标签质量

End to End

Soft Teacher基本思路：对未标记的图像进行标记，然后通过标记的几个伪标签训练检测器.

具体而言：

  1. 采样标注和未标注图片形成Batch
  2. 双模型：检测（student）、标记（teacher）
  3. EMA：T模型是S模型的EMA

这种方式避免了多阶段方案实现上的复杂，同时实现了飞轮效应==S、T相互加强;

此外Soft Teacher直接对学生模型生成的所有候选框进行评估，而不是使用伪框来为这些候选框进行分类回归。 这样能使用更多的直接监督信息

具体而言：

  1. 使用高阈值来分割前景，确保不会错误的将背景分类成前景，确保正伪标签的高精度；
  2. 使用可靠性度量来加权背景候选的损失；
  3. 教师模型产生的检测分数可以很好的作为可靠性度量

Box Jitter为了更可靠的训练学生网络的本地分支，指的是：

  • 我们对前景框候选进行多次抖动
  • 根据教师模型的位置分支对这些候选进行回归
  • 将回归框的方差作为可靠性度量
  • 可靠性高的用来训练

Semi-Supervised Learning in Image Classification & object detection

  • consistency based
  • pesudo-label based

new idea：使用弱数据增强生成伪标签和强增强来学习检测模型，区分两部分工作

Object Detection

Based on Faster R-CNN to compare with other method

Methodology

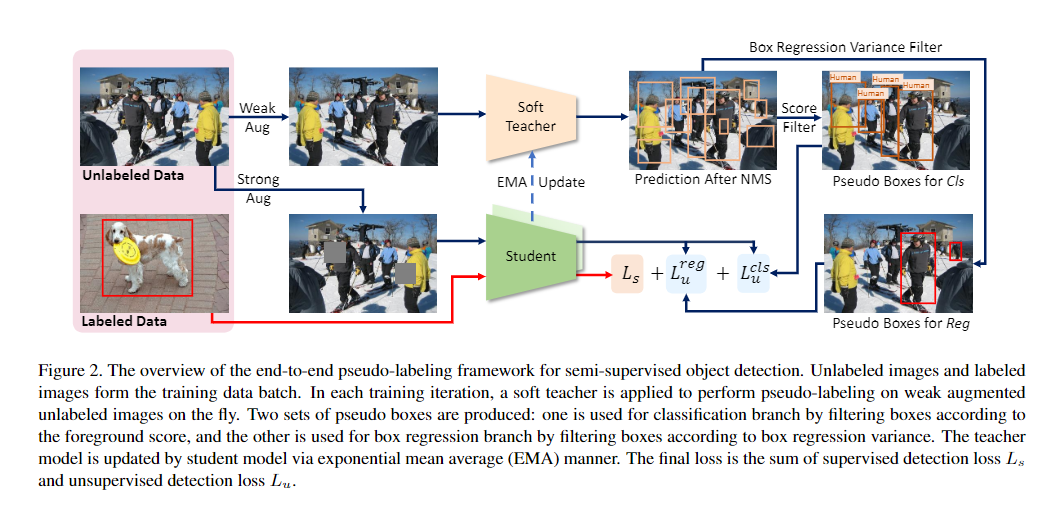
可以从下面的图中看出基础的实现逻辑：

Framework

训练（Loss）是基于Batch进行，对于标记数据和未标记数据的损失处理时分开的， 对于未标记数据，我们需要通过教师模型来得到一个softlabel，包括分类和回归两个任务，然后得到最终的损失值。

$$ L = L_s + \alpha L_u $$

image-20210914152516997

两者都要通过各自的图像数量进行归一化，以标注数据为例

$$ L_s = \frac{1}{N_l}\sum_{i=1}^{N_l}(L_{cls}(I_l^i)+(L_{reg}(I_l^i)) $$

如何启动教师模型：

随机初始化学生模型和教师模型，后续通过学生模型的EMA来进行教师模型的更新。

目标检测的伪标签定义：

教师模型检测后NMS消除冗余，然后使用阈值来抑制非前景的候选；

获取高质量的伪标签：

对教师模型的伪标记使用弱增强，学生模型训练使用强增强

Soft Teacher

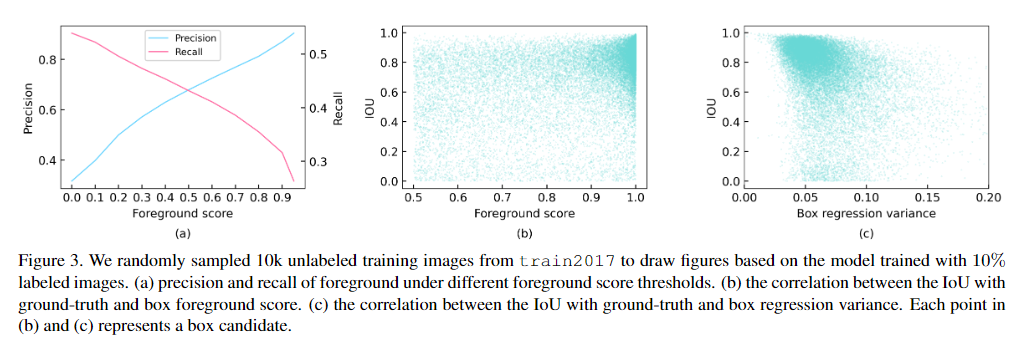
检测器的性能取决于伪标签的质量，如果在前景分数上使用较高的阈值过滤掉大部分学生生成的低置信度候选框可以得到更好的结果，当阈值设置为0.9时性能最佳，但是召回率迅速下降。

  • 一般方法：使用学生生成的候选框和教师生成的候选框的IoU来分配前景和背景，可能会损坏性能。
  • 软教师：我们评估学生生成的候选框作为真实背景的可靠性，用于衡量背景分类损失；
$$ b^{fg}_i $$
、
$$ b^{bg}_i $$
分别是分配为前景的框和分配为背景的框，具有可靠权重的伪标记图像的分类损失定义为：
$$ \mathcal{L}_{u}^{\mathrm{cls}}=\frac{1}{N_{b}^{\mathrm{fg}}} \sum_{i=1}^{N_{b}^{\mathrm{fg}}} l_{\mathrm{cls}}\left(b_{i}^{\mathrm{fg}}, \mathcal{G}_{\mathrm{cls}}\right)+\sum_{j=1}^{N_{b}^{\mathrm{b}_{b}}} w_{j} l_{\mathrm{cls}}\left(b_{j}^{\mathrm{bg}}, \mathcal{G}_{\mathrm{cls}}\right) $$

image-20210914165532071

$$ w_j = \frac{\gamma_j}{\sum_{k=1}^{N_b^{bg}}\gamma_k} $$
$$ \mathcal{G}_{cls} $$
表示用于分类（教师生成的）伪框集，
$$ l_{cls}() $$
是框分类损失，
$$ r_j $$
是第j个背景的可靠性分数；

我们通过教师模型产生的背景分数可以很好的代替可靠性：

  • 使用教师模型（BG-T）通过检测头来获取样本的背景分数

还研究了：学生模型，学生模型和学生模型之间的差异

Box Jittering

图三b可以看到，候选框的定义准确率和前景分数不是一个正相关的关系，他不一定能提供准确的定位信息。

需要更好的候选框，在教师生成的候选框bi上做抖动采样，将抖动框输入教师模型获得调整后的框

$$ \hat{b_i} = refine(jitter(b_i)). $$

抖动 $N_{jittle}$ 次后得到 ${\hat{b}_{i,j}}$ 集合，然后将可靠性定义为box回归方差：

$$ \overline{\sigma}_i = \frac{1}{4}\sum_{k=1}^4\hat{\sigma}_k $$

其中：

$$ \hat{\sigma}_k = \frac{\sigma_k}{0.5(h(b_i)) + w(b_i)} $$

较小的框回归方差表示较高的本地可靠性，但是大量的计算也是不可忍受的，所以我们一般只计算前景分数大于0.5的框的可靠性

回归方差计算：

$$ \mathcal{L}_{u}^{\mathrm{rcg}}=\frac{1}{N_{b}^{\mathrm{fg}}} \sum_{i=1}^{N_{b}^{\mathrm{f}_{8}}} l_{\mathrm{reg}}\left(b_{i}^{\mathrm{fg}}, \mathcal{G}_{\mathrm{reg}}\right) $$
$$ \mathcal{L}_{u}=\frac{1}{N_{u}} \sum_{i=1}^{N_{u}}\left(\mathcal{L}_{u}^{\mathrm{cls}}\left(I_{u}^{i}, \mathcal{G}_{\mathrm{cls}}^{i}\right)+\mathcal{L}_{u}^{\mathrm{rcg}}\left(I_{u}^{i}, \mathcal{G}_{\mathrm{rcg}}^{i}\right)\right) $$

Experiment

实验细节