Created by: Aiken H Desc: GAME, RL Finished?: Yes Tags: Paper
《Master Complex Control in MOBA Games with Deep Reinforcement Learning》 论文阅读笔记
@Aiken H 2021.06
Introduction and Related Research.
MOBA游戏的复杂度和状态空间都远比以前的围棋之类的运动更大,所以难度会更大一些
早一些的游戏ai使用的是(2015) Deep Q-Network 通过 supervised learning and self-play 结合的训练策略在围棋上击败了专业人类,而最近更多的使用了DRL(Deep Reinforcement Learning)的方法在近几年被进一步的应用。
Neural Network Architecture Include
Contributions
- the encoding of Multi-modal inputs 多模态输入
- the decoupling of inter-correlations in controls 控制内关联解码
- exploration pruning mechanism 剪枝设置
- Action mask for efficient exploration ❓效率
- attack attention(for target selection) Attention机制做目标选择
- LSTM for learning skill combos LSTM 机制做技能释放和链接
- Optimize by multi-label proximal policy algorithm(improved PPO)
- dual-clip PPO 帮助训练的收敛
present a systematic and thorough study
develop a deep reinforcement learning framework which provides scalable and off-policy training
we develop an actor-critic neural network
跳转上面的网络架构
Framework Design
(S.O.A.P, $\gamma$ , $\tau$ , $\rho_0$ ) to denote infinite-horizon : 使用元组去模拟整个动态强化的过程,过程主要的是最大化累计reward
S 状态空间 O 观察状态空间 A 动作空间 $\rho_0$ 初始状态分布 $\gamma$ 折扣系数
目标MAX: $\mathbb{E}[\sum_{t = 0}^{T} \gamma^t \tau(s_t,\alpha_t)]$
$\tau: S \times A \rightarrow \mathbb{R}$ 奖励函数
$\pi: O \times A \rightarrow [0,1]$ 策略
$P:S\times A \rightarrow S$ 状态转移分布
SUMMARY: This Part is about the basic rule of the RL setting.
System Design
The whole system and workflow design will be shown on this part
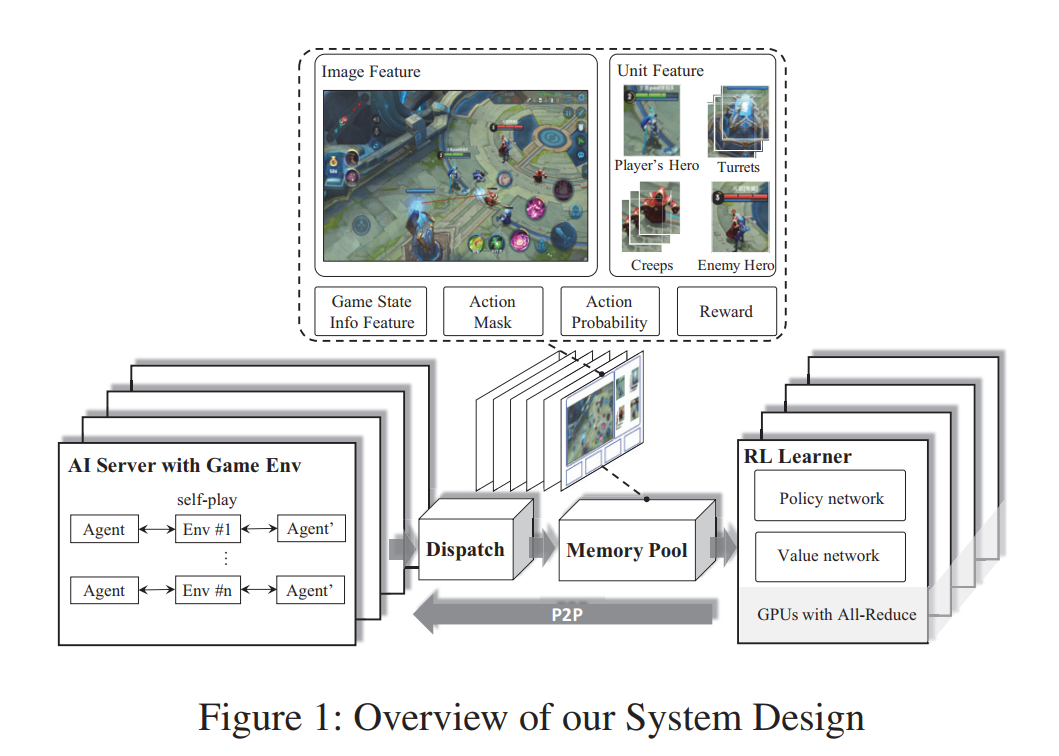
由于MOBA游戏复杂的Agent(Players和Characters) 会带来高方差的随机梯度,所以再这种模型的训练中,我们可能会需要一个大的Batach Size来防止Invariant Shift的这种现象,同时并加速训练的有效和收敛性。于是我们设计了一个规模可变,弱耦合的网络架构。
模型整体由四个部分组成:RL-Learner、AI-Server、Dispatch-Module(调度)、Memory-Pool(记忆池)
- AI-Server::与环境进行交互模拟(self-play)
- RL Learning:核心学习网络
- Memory Pool:数据存储,为RL提供训练和搜索的实例
- Dispatch:数据的收集,压缩,传输
- 模块之间相互解耦,可以灵活配置,
Module Detail
AI-Server
- 传统策略:提供了游戏环境和AI模型之间的交互逻辑,通过相互镜像的策略来进行self-play,从而生成episodes.
- 对手策略:基于游戏状态中提取的特征使用玻尔兹曼搜索,预测英雄行文(基于softmax的分布采样,发送给CPU执行),返回reward和下一个state
- CPU版本的FeatherCNN,转换到LOCAL上进行inference
Dispatch Module
- 和多个AI-Service绑定,是一个收集数据样本的服务器,主要包括:奖励,特征,动作概率等
- 将这些数据压缩和打包,然后发到内存池中
Memory Pool
- 服务器:内部实现为用于数据存储的内存高效循环队列
- 支持不同长度的样本,以及基于生成时间的数据采样
RL Learner
- 分布式训练环境,为了使用Big Batch,使用多个RL Learner并行的从Memory Pool 获取数据,然后通过ring allreduce算法来集成梯度
- 通过共享内存(而不是socket)和pool来进行数据交换,从而减少IO需求
- P2P的在策略更新和AI service进行快速同步
SUMMARY: 经验生成和参数学习是分离的,以及Memory和Dispath的架构,能够使得算法能够很容易的拓展到百万歌CPU内核和数千个GPU。
Algorithm Design
An Actor-Critic Network 用来建模游戏中的动作依赖关系
网络架构
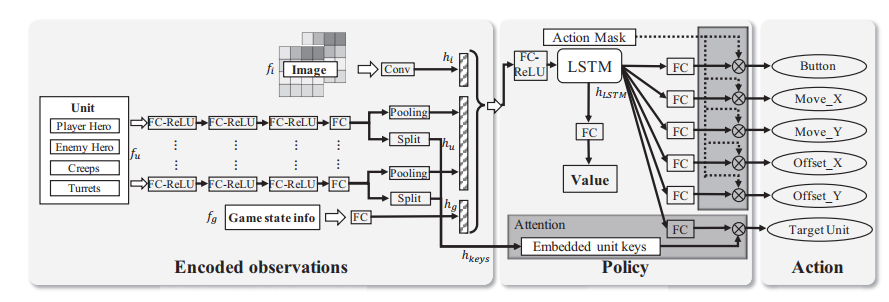
由下图说明了网络的状态和动作,为了有效的训练这个网络,提出了一些新颖的策略:目标注意力机制(选择目标);LSTM用来学习技能combo,和动作选择;控制依赖解耦来建立一个PPO;(先验引入)基于游戏知识的剪枝(Action mask);优化PPO成dual-clipped PPO 保证大批次和大偏差的收敛性
对图像、Unit、GameInfo分别提取特征后整合成固定长度的Feature,通过LSTM(考虑时间维度的表征)得到最终的表征,然后通过FC对特征进行分类解码(也可以说是预测把),同时基于状态编码的注意力机制来整合出对象预测,
- p(t|a)是units上的注意力分布,维度是状态中的单元数。
- 为了解决多标签策略网络中,同一个动作不同标签之间的关联显示建模困难的问题,独立处理一个动作中的每个标签解耦他们的相互关联。
原始的PPO objective:E:有限批次的经验平均值,其余的参见上面的对照表
参数解耦之后可以看到:
有两个优点:简化策略的结构(不考虑相关性);增加策略的多样性,为了多样性,我们开始的训练过程中,随机了初始化agent的位置。
缺点:进一步增加的策略训练的复杂度,所以通过action mask来进行简化,在最终输出层来合并动作元素之间的相关性,从而修建需要的策略搜索空间,
Dual-clip PPO
令 $\tau_t(\theta) = [\frac{\pi_{\theta}(a_t|s_t)}{\pi_{\theta_{old}}(a_t|s_t)}]$ ,由于这个值可能会很大,导致过大的策略偏差,为了缓解这个问题,我们引入
来惩罚政策的极端变化,但是另一种情况下的极端值也会带来无界偏差,所以还有另一端的优化,其中c>1是一个下线常数