LT-Collections

@AikenHong 2021

Code of must of those methods We will analysis those tricks on LT situation, and Analysis why it works. 在进行LT矫正的任务中，有几种常见的trick在各种模型中被使用，我们会对这几种不同的trick进行介绍和分析。

其实在数据量少这一方面LT和Few-Shot是有一定的OverLap的,可以参考以下那边的思路perhaps

Introduction

LT

通常情况下这种严重的类别不平衡问题会使得模型严重过拟合于头部，而在尾部欠拟合

首先介绍 bag of tricks 这篇论文中总结了一些常用的Trick，并组合出了最佳的一套trick

经过该文实验总结，Trick组合应该是[1]`：

  • 在前几个epoch应用input mixup数据增强，然后后面fine-tuning;
  • (基于CAM的)重采样来重新训练分类器;

实际上就是MixUp + Two-Stage的策略，后续对Mix-up这个策略带来的作用要进行补充了解一下

Rebalance

对于ReBalance的方法，实际上就是从 data和 update两个角度来缓解Unbalance本身，通过从数据量上达到重新均衡，或者基于Loss使得bp过程中赋予Tail更高的权重来达到优化过程的平衡。

前者称为rebalance，后者则为reweight.

reweighting

这一部分在实际设计上的体现主要是通过对Loss的重新构造而成，通过对Loss的构造来实现区分的BP权重.

  1. 代价敏感softmax交叉熵损失CS_CE: 在ce前乘最小训练图像数目与每个类别图像数目的比值，相当于更注重少类样本
$$ \mathcal{L}_{CS\_CE}(\mathbf{z}, c)=-\frac{n_{\min }}{n_{c}} \log \left(\frac{\exp \left(z_{c}\right)}{\sum_{i=1}^{C} \exp \left(z_{i}\right)}\right) $$
  1. Focal Loss：设置 $\alpha$ 和 $\beta$ 来控制少数类和难分类别对损失的贡献：
$$ \mathcal{L}_{\text {Focal }}(\mathbf{z}, c)=-\sum_{i=1}^{C}\left(1-p_{i}^{t}\right)^{\gamma} \log \left(p_{i}^{t}\right) $$
  1. 类别平衡损失：就是在基本的损失（CE，FOCAL）前加入一个衡量权重，其中 $\beta$ 是一个超参数，来衡量有效的信息
$$ \mathcal{L}_{CB\_Focal}(\mathbf{z}, c)=-\frac{1-\beta}{1-\beta^{n_{c}}} \sum_{i=1}^{C}\left(1-p_{i}^{t}\right)^{\gamma} \log \left(p_{i}^{t}\right) $$
  1. Logit Abjustment[3]:
$$ \ell(y, f(x))=\alpha_{y} \cdot \log \left[1+\sum_{y^{\prime} \neq y} e^{\Delta_{y y^{\prime}}} \cdot e^{\left(f_{y^{\prime}}(x)-f_{y}(x)\right)}\right] $$

rebalance

实际上就是对少类或者多类的数据重新做均衡，方法的本质差别一般都不是特别大

  1. 随机过采样：随即重复少数类别的样本来使得样本均衡
  2. 随机降采样：随机删除多数类别的样本使得样本均衡
  3. 样本平衡采样：应该值得就是1-2 IB-Sampling
  4. 类别平均采样: 对类别进行统一采样，每个类别被采样的概率都一样(Q=0)，然后从每个类别中有放回的随机采样实例，从而构建平衡的数据集
$$ p_j = \frac{n_j^q}{\sum_{i=1}^C n_i^q} $$
  1. 平方根采样(Q=0.5)
  2. 逐步平衡采样：先对多个epoch进行实例平衡采样（上式q=1，也就是没有任何平衡操作的采样），然后再剩下的epoches中进行类别平衡采样。这种采样方式需要设置一个超参数来调整从哪一个epoch开始变换采样方式。也可以使用更软的阈值，即随着epoch的增加来逐渐调整实例平衡采样（IB）和类别平衡采样所占的比例，如下面公式所示。
$$ P_j^{PB} (t) = (1-\frac{t}{T})P_j^{IB} + \frac{t}{T}P_j^{CB} $$

two-stage

在Unbalanced的Data上Pretrain一个特征提取器，然后再rebalance（IB，CB）的数据集上对Classifier进行重新训练（调整），（and | or）对齐，校准（disalign，causal）来提升LT的性能的方法

motivation

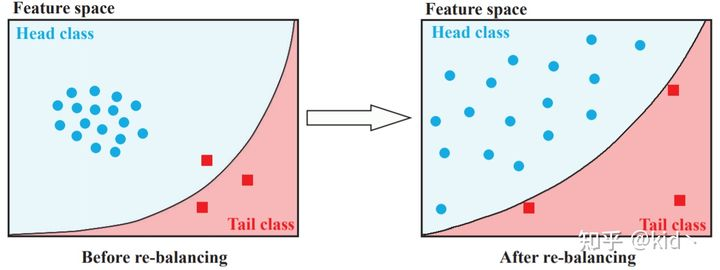
rebalance

但是这些rebalance的方法通常会带来以下两个问题[2]：

  • rebalance之后分类器会倾向于分类正确的尾部样本，导致对于头部有一定的bad influence（欠拟合），对尾部过拟合
  • rebalance方法会显著的促进分类器的学习，但是会损害深度特征的表示能力，如上图所示，分类器学到的分界面更好，但是特征的表示却更加的松散了

我认为rebalance的策略确实会使得Clf学的更好的分界面，减少偏向性，但是不至于在尾部过拟合，这一部分分析最重要的应该是rebalance对于特征空间的Bad Influence，这可能就是Two Stage的来源。

Absl

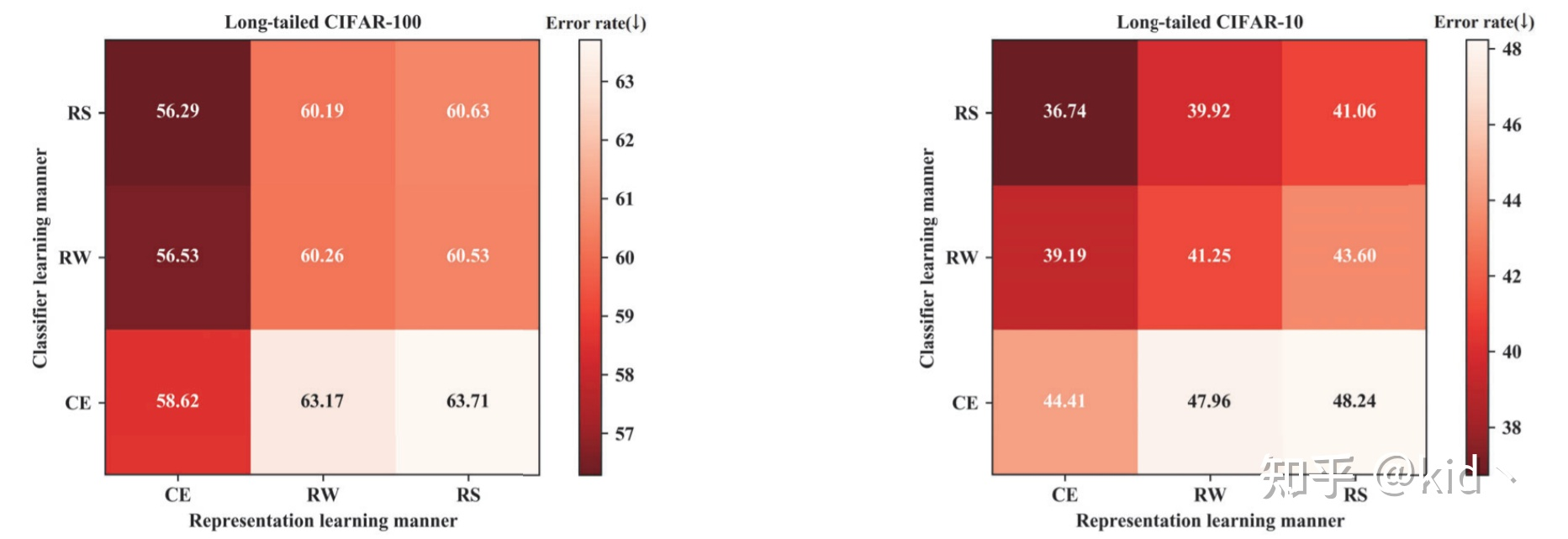
于是作者为其设计了一些消融实验：CE指的是长尾，RW，RS指的是使用的rebalance的数据。

可以发现在Backbone上使用Unbalance的数据而在Clf上使用Resampler的数据效果是最好的，这种two-stage的解耦两阶段的训练策略展现了一个有希望的结果。

这种两阶段的方式，我认为在第二阶段的时候也要对特征进行微调来适应当前的分布，不过很多的方法都是直接只对分类器进行调整，我们可以对两种方式进行测试

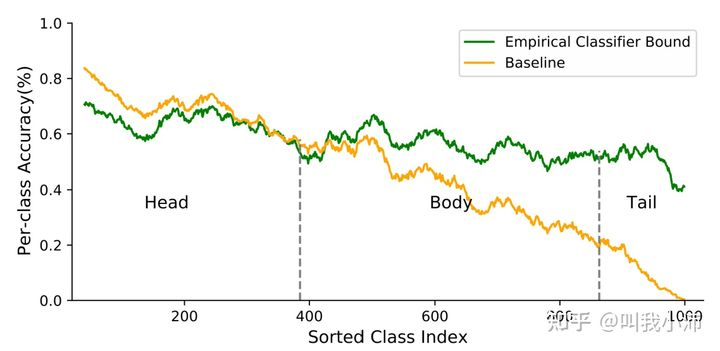
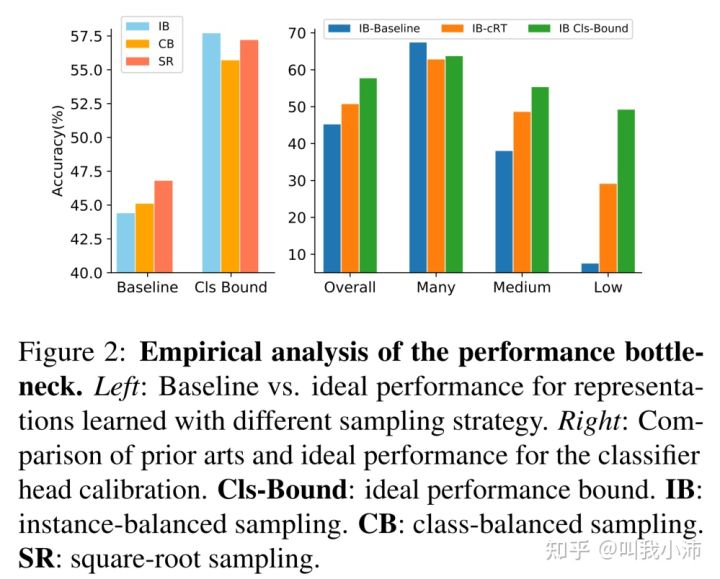
下图显示了fix-two-stage和baseline对比[5]

two-stage

下图展示了理想的two-stage结果与显示方法之间的距离[5] cls-bound是再fix特征后，用完全均衡的数据集训练分类器得到的结果，由此带入第二张图的绿色的线，可以知道，现有长尾方法的性能瓶颈（未使用two-stage），仍然在特征空间中的有偏差的决策边界。

ideal-real

基于这些分析,我们认为，在得到一个强有力的特征表示后，我们可以将问题归化到分类器上，基于这点假设，我们可以结合我们的自监督模块来对该方法进行归化。

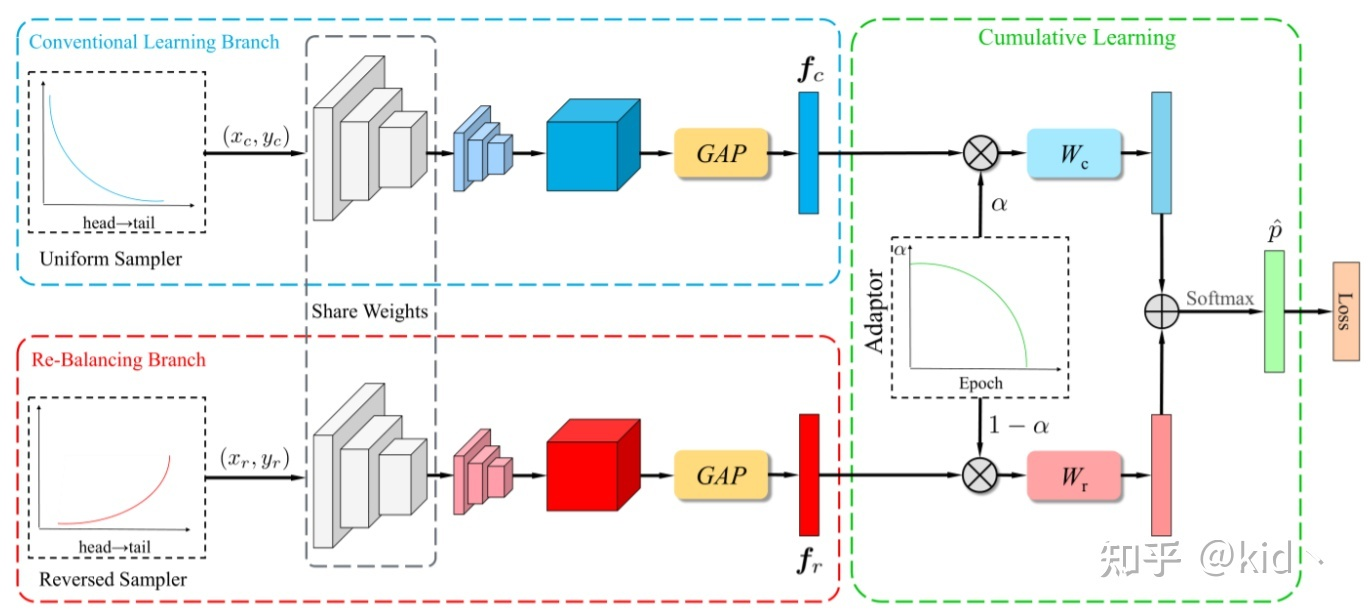
BBN structure

BBN
Share Weight of Backbone，Using diff dataset to get diff feature. Then we using $\alpha$ to Combine the logits and calculate the loss.

$$ z = \alpha * W_c^T * f_c + (1-\alpha) * W_\gamma^T * f_\gamma $$
$$ L = \alpha * l(softmax(z),y_c) + (1-\alpha) *l(softmax(z),y_\gamma) $$

在上述的流程图中W代表的是两个不一样的数据优化器，基于这样的设置最终就能区分两部分的优化。

但是这个方法为我们带来的最大的启发还是在于区分两阶段中学习的重点，backbone需要在一个unblance的条件下学习一个更为通用的表征，而Cls需要矫正偏差。不平衡的情况下可能能学到一个很好的通用表征，这一点就是我们使用自监督的一个重要原因。

Decoupling

==Train BB and Fixed then Train CLF== 此外坐着发现全连接的weight和norm和对应类别的样本数正相关，所以在第二部最后将分类器改为归一化的分类器，文中的两种设计是：

  1. $\overline{W_i}=\frac{w_i}{\lVert W_i \rVert^T}$
  2. $\overline{W_i}=\frac{w_i}{f_i}$

其中2利用fixed第一步分类权重 $w_i$ ,对每个类学习了一个加权参数 $f_i$

better-calibration

但是这种两阶段的方式也不是没有代价的，他会带来比较严重的校准错误(Calibration)，也就是我们预测的概率和实际的相似度之间的一致性。

（BTW评估校准错误的指标 $ECE=\sum_{b=1}^B\frac{|S_b|}{N} |acc(S_b) - conf(S_b)|$ ，将数据分为b组，S_b是落入b区间的样本集合)

本文主要测试了MixUP在两阶段训练中的作用，以及提出了：

  1. 标签感知平滑损失，实际上就是cb_ce的半泛化形式：
$$ \begin{gathered} l(\boldsymbol{q}, \boldsymbol{p})=-\sum_{i=1}^{K} \boldsymbol{q}_{i} \log \boldsymbol{p}_{i} \\ \boldsymbol{q}_{i}= \begin{cases}1-\epsilon_{y}=1-f\left(N_{y}\right), & i=y \\ \frac{\epsilon_{y}}{K-1}=\frac{f\left(N_{y}\right)}{K-1}, & \text { Otherwise }\end{cases} \end{gathered} $$

$\epsilon_y$ 是y(gt)的一个小平滑因子,数目与类别的样本数有关，并提出了几种函数形式，来优化这个损失 2. BN的移位学习，由于两阶段的数据集不一致，所以normalize的参数是需要学习变化的（均值和方差）

具体的数学分析和推导，后续根据论文理解了再来补充

DisAlign

基于上述对于方法的分析，该文章着重于对于分类器进行校准，具体的思路是基于利于平衡预测的类别分布来对分类器的输出进行匹配，矫正；简单的说利用类别先验和输入数据学习类别的决策边界。 具体由两部分构成(重构预测的概率输出，建立理想分布，使用KL散度计算损失)

  1. 自适应配准函数
$$ \begin{gathered} s_{j}=\alpha_{j} \cdot z_{j}^{o}+\beta_{j}, \quad \forall j \in \mathcal{C} \\ \hat{z}_{j}=\sigma(\mathbf{x}) \cdot s_{j}+(1-\sigma(\mathbf{x})) \cdot z_{j}^{o} \\ =\left(1+\sigma(\mathbf{x}) \alpha_{j}\right) \cdot z_{j}^{o}+\sigma(\mathbf{x}) \cdot \beta_{j} \\ p_{m}(y=j \mid \mathbf{x})=\frac{\exp \left(\hat{z}_{j}\right)}{\sum_{k=1}^{C} \exp \left(\hat{z}_{k}\right)} \end{gathered} $$
  1. 广义重加权校准 理想的分布的计算方法如下，定义说的不是很好，最好还是参考一下代码
$$ \begin{gathered} p_{r}\left(y=c \mid \mathbf{x}_{i}\right)=w_{c} \cdot \delta_{c}\left(y_{i}\right), \quad \forall c \in \mathcal{C} \\ w_{c}=\frac{\left(1 / r_{c}\right)^{\rho}}{\sum_{k=1}^{K}\left(1 / r_{k}\right)^{\rho}}, \quad \forall c \in \mathcal{C} \end{gathered} $$

最终的损失计算方程如下：

$$ \begin{aligned} \mathcal{L} &=\mathbb{E}_{\mathcal{D}_{t r}}\left[\mathcal{K} \mathcal{L}\left(p_{r}(y \mid \mathbf{x}) \| p_{m}(y \mid \mathbf{x})\right)\right] \\ & \approx-\frac{1}{N} \sum_{i=1}^{N}\left[\sum_{y \in \mathcal{C}} p_{r}\left(y \mid \mathbf{x}_{i}\right) \log \left(p_{m}\left(y \mid \mathbf{x}_{i}\right)\right)\right]+C \end{aligned} $$

==训练的具体策略== 1）在第一阶段，在不平衡数据集上使用实例平衡 ( instance-balanced ) 采样策略实现特征提取器和原始分类头的联合学习。此时由于不平衡的数据分布，学习到的原始分类头是严重有偏的。

2）在第二阶段，我们在特征提取器参数固定不变的情况下关注分类头以调整决策边界，引入了自适应配准函数 ( adaptive calibration function ) 和广义重加权 ( generalized re-weight ) 策略来配准各类概率。

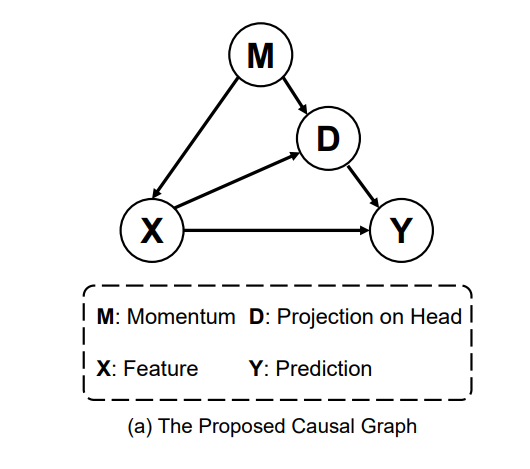
Caucal Analysis

基于two-stage的这种现象，然后分析机器和人学习的区别，认为带来偏差的元凶在于Optim优化算法，为此，该文章构建因果图，从而去除在模型更新过程中由动量带来的偏差效应。

"keep good and remove bad momentum"[7]

causal

$v_t = \mu · v_{t-1} + g_t$ , $\theta = \theta_{t-1} - lr · v_t$

要调用这个方法的话，我们就需要

  1. 将训练的CLF修改成Multi-Head并Normlize，参考Decouple.
  2. 训练过程中统计移动平局特征 $\overline{x}$ ，将其单位方向看成头部倾向.
  3. 测试的过程中修正logits即可

具体公式参考对应的解析和代码实现;

和自监督结合的话，只需要在微调的阶段进行统计和修正即可，毕竟是一个一阶段的方式。

Contrastive

这一部分考虑一些和对比学习，或者说自监督学习耦合的方法来进行分析。

为何将这两者放到同一个章节中？ 因为这两者企图从表征的层面，为LT任务，带来增益，得到一个可分的特征空间基于良好的特征表达，进而解耦的来训练一个更好的CLF。

如果我们假设我们能得到一个高维线性可分的特征空间，对于长尾的样本带来的训练偏差（决策面偏差）是否可以通过对于特定类别的Margin-Like的Loss设置，达到一个类似Balance的效果，这一点上实际上可能和Align和校正的思想有点相似。但是我们是为了让分类器空间中的分界面在小样本的束缚下变得更加的合理。

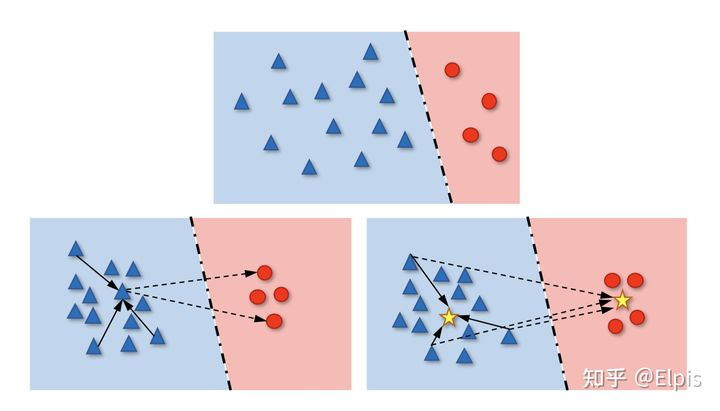
从分界面的角度看LT的情况：（上面是普通CE，下面是Contrastive Learning）

CL
在数据量出现较大的差异的情况下，由于蓝色的数目更多更杂，所以实际上分界面可能会沿着蓝色数据的边界做切分（overfit），在这种Class-Level的过拟合下，就会导致对于少数类别的分类结果很差。

而下方的对比学习就是一样的解决方案，他试图将同一类的数据聚拢在一起，将不同类的距离尽可能的拉远，这样会使得在空间中的决策面更加的鲁棒也已于区分，虽然可能会一定程度上减少蓝色的表现，但是红色的表现会因此大大的提升。

hybird contrastive

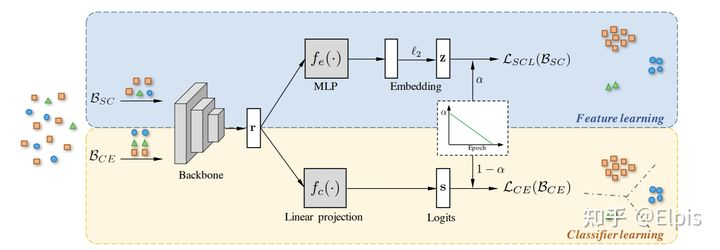
该文章[9]的基本架构上实际上参考的就是BBN的epoch-params在two-stage中集成 supervised contrasive Loss，具体框架可以看下面这图：

hybird-contrastive learning for lt
他的设计思想很容易从这张图中领会，损失函数的表达显然如下

$$ L_{hybird} = \alpha · L_{SCL}(B_{SC}) + (1-\alpha) · L_{ce}(B_{CE}) $$

在这里要注意SC和自监督中使用的区别在于，自监督学习的过程中没有标签，所以只能将自己作为Positive，而在SC的时候，同类的样本之间应该都作为Positive

$$ \mathcal{L}_{S C L}\left(\mathbf{z}_{i}\right)=\frac{-1}{\left|\left\{\mathbf{z}_{i}^{+}\right\}\right|} \sum_{\mathbf{z}_{j} \in\left\{\mathbf{z}_{i}^{+}\right\}} \log \frac{\exp \left(\mathbf{z}_{i} \cdot \mathbf{z}_{j} / \tau\right)}{\sum_{\mathbf{z}_{k}, k \neq i} \exp \left(\mathbf{z}_{i} \cdot \mathbf{z}_{k} / \tau\right)} $$

鉴于SC的计算复杂度要和整个Epoch的数据进行对比，需要大量的显存空间，在这方面作者将其改进为PSC，其实也就是将每个class计算一个prototype，然后基于原型去计算这个相似性损失

$$ \mathcal{L}_{P S C}\left(\mathbf{z}_{i}\right)=-\log \frac{\exp \left(\mathbf{z}_{i} \cdot \mathbf{p}_{y_{i}} / \tau\right)}{\sum_{j=1, j \neq y_{i}}^{C} \exp \left(\mathbf{z}_{i} \cdot \mathbf{p}_{j} / \tau\right)} $$

在这里这个Prototypical需要正则化到单位元中，这样能快速计算相似性损失，也不会需要大量的现存。

可以参考的点主要就在于损失的设计和框架上的这种分epoch机制了，但是基于自监督的方式的话，可能不是很用的上这一点，但是我们可以考虑怎么结合这个loss去做对应的分类器。

The value of labels

这一篇文章是将自监督学习和半监督学习应用到长尾分布的问题上，文章对应的仓库中可以get预训练模型和很多对应的数据，同时验证了下面两种策略都可以大大提升模型的效果，包括和之前的各种策略进行耦合。

  • 半监督：利用更多的无标注数据
  • 自监督：不利用任何其他数据，使用长尾分布的数据进行自监督训练

后续的实验过程中我可能也会遵循该设计，或者使用的是全数据的自监督预训练。

考虑尾部标签本身的意义，想要利用尾部的标签信息，又不受偏差的影响，实际上就是使用自监督进行预训练，然后后面使用各种方法兼容的一个策略。

Self-Supervised

MixUp in LT

将MixUP应用在LT中，试图"以使其具有更高的泛化性，以及降低模型本身的置信度"[4], 经过实验表明，仅在Stage1使用MixUP，在Stage2的第二阶段使用几个epoch的Mixup的效果可能会更好。

在这里可能也要考虑一下CutMix方法

Conclusion

实验结果汇总

基于BackBone对这些方法的实验结果( $Top1 Acc$ )进行汇总，作为我们后续研究的参照：在进行实验的时候，我们需要首先调整好BenchMark，基于Benchmark做的改进才能和对应的方法进行对比。

整理原则：

  1. 对应的论文则由该论文本身为主，后续和LT的仓库进行对比分析；
  2. 最主要需要对比的应该是ce情况下的指标，这是我们最重要的，当这个指标对齐后，我们就可以和这些方法同台竞技了。
Dataset->LT-Cifar-100<-->LT-CIfar10<-Backbone
Factor(Exp)10050101005010ResNet32
RESULT------
CE38.3243.8555.7170.3674.8186.39-
Focal Loss38.444.356.870.476.786.7-
MixUp39.545.058.073.177.887.1-
CB Loss39.645.258.074.679.387.1-
BAGS-After47.8351.69-73.5979.03--
SSL-Uniform40.4045.0457.0773.5078.2087.72
SSL-Balanced43.0647.0958.0676.5380.487.72
LDAM42.046.658.777.081.088.2-
BBN42.5647.0759.1279.8282.1888.32-
Causal44.150.359.680.683.688.5-

Reference

阅读过程中还看到一些什么BAGS，进行数据分组的方法，这个方法肯定不会在我们的框架中使用，但是我们可以分析一下这种分组训练为什么会对长尾的场景存在差异。

  1. ⭐“Bag of Tricks for LT Visual Recognition with Deep Convolutional Neural Network” ZHIHU
  2. ⭐“BBN: Bilateral-Branch Network with Cumulative Learning for Long-Tailed Visual Recognition” ZHIHU CVPR20
  3. ❓“Long-Tail Learning via Logit Abjustment” ICLR 20 zhihu1 | zhihu2
  4. “Improving Calibration for Long-Tailed Recognition” CVPR21 zhihu
  5. ⭐“Distribution Alignment: A Unified Framework for Long-tail Visual Recognition” CVPR21 zhihu | zhihu2
  6. “Decoupling Representation and Classifier for Long-Tailed Recognition” ICLR20
  7. “Long-Tailed Classification by Keeping the Good and Removing the Bad Momentum Causal Effect” NIPS20 | zhihu
  8. “Rethinking the Value of Labels for Improving Class-Imbalanced Learning” NIPS20| zhihu
  9. “Contrastive Learning based Hybrid Networks for Long-Tailed Image Classification” CVPR21 zhihu

总结性串讲：

  1. LT-Classification