经典深度学习与机器学习算法

LINK1

深度学习部分

DenseNet

任意的两层之间都存在直接的链接，每一层的输入都是前面的所有层的输出的并集，而该层学习的特征图也会是后面所有层的输入，DenseBlock中需要Feature_map保持一致；

Block与Block之间的降采样则使用transition layer，使用BN，1*1的 conv，Pooling来降维

优缺点：

1. 省参数，省计算
2. 抗过拟合，泛化能力强
3. 需要保存Feature占显存

EfficientNet

针对卷积神经网络的模型拓展，可以通过：1

1. 增加网络规模可以、 增加模型宽度，增加模型深度，增加输入图像的分辨率，但是如何去人工调整这个比例和参数，比较麻烦，
2. 实验发现ConvNet缩放过程中平衡网络宽度、深度、和分辨率的维度是很重要的
3. EfficientNet就是对这些的合理组合，复合型的模型扩展技术集合神经结构搜索技术获得

关键技术复合扩张技术

所以本文提出了复合扩张方法，这也是文章核心的地方，

1. 固定公式中的φ=1，然后通过网格搜索（grid search）得出最优的α、β、γ，得出最基本的模型EfficientNet-B0.
2. 固定α、β、γ的值，使用不同的φ，得到EfficientNet-B1, …, EfficientNet-B7

φ的大小对应着消耗资源的大小，相当于：

1. 当φ=1时，得出了一个最小的最优基础模型；
2. 增大φ时，相当于对基模型三个维度同时扩展，模型变大，性能也会提升，资源消耗也变大。

bottleneck

Bottleneck layer又称之为瓶颈层，使用的是1*1的卷积神经网络。之所以称之为瓶颈层，是因为长得比较像一个瓶颈。

如上图所示，经过 $11 conv$ ，中间那个看起来比较细。像一个瓶颈一样。使用 $11$ 网络的一大好处就是可以大幅减少计算量。深度可分离卷积中，也有这样的设计考虑。如果想具体了解如何大幅减少计算量的话，可以参考参考资料[2]

Xavier参数初始化方法

已经写在笔记上了，但是还要补充的，或者说是理清楚的是怎么推导的或者为什么这么干的，还有其他的初始化方法之间的区别什么的

模型压缩

为了研究小而快的机器学习模型：1. 对复杂模型进行压缩 2. 直接设计小模型得到训练

轻量网络：MobileNet

主要的网络架构：是使用depthwise separable convolution也就是xception中提到的这种，双分离的卷积

然后使用：ReLU6激活函数（限制最大输出为6）

过程中不使用pooling直接使用stride=2进行下采样

基本的组件如图所示： 最后用avg pooling从 $771024 $ 到 $111024$

对其进行瘦身：

• 按比例缩放特征图的大小
• 按比例缩放通道数

核心的计算量实际上在 $1*1 conv$ 这个全通道密集卷积的操作上

V2：

• 引入了shortcut（残差结构）

• 在进行depthwise之前先用 $1*1$ 扩张feature_map的通道数

  是为了提升效果，参数量比1还是稍微增加了，

  这里的1*1和resnet中的是完全相反的：

  残差模块：11降维 33卷积 11升维 反残差模块：11升维，33卷积，11降维

  原因：因为depthwise卷积不能改变通道数，因此特征提取受限于输入的通道数，所以将通道数先提升上去。文中的扩展因子为6。

• pointwise之后的relu改成了Linear激活函数，防止relu破坏特征

  原因：relu造成的低维度数据塌陷
  

  https://www.sohu.com/a/307566264_100024677

  就是当低维信息映射到高维，经过ReLU后再映射回低维时，若映射到的维度相对较高，则信息变换回去的损失较小；若映射到的维度相对较低，则信息变换回去后损失很大。因此，认为对低维度做ReLU运算，很容易造成信息的丢失。而在高维度进行ReLU运算的话，信息的丢失则会很少。
  因为relu函数小于0时候，值为0，是有信息损耗的，而线性激活函数没有信息损耗

轻量网络：Shufflenet

V1 带Pytorch

ShuffleNet的核心是采用了两种操作：pointwise group convolution和channel shuffle，这在保持精度的同时大大降低了模型的计算量。

缓解 $1*1 conv$ 的计算量，也使用channel sparse connection，但是这种group convolution 也有弊端：特征图之间不通信，所以我们就channel shuffle（均匀打乱）

图3.(a)是一个普通的带有残差结构的深度可分离卷积，例如，MobileNet [5], Xception [6]。ShuffleNet v1的结构如图3.(b)，3.(c)。其中3.(b)不需要降采样，3.(c)是需要降采样的情况。

V2:

1. G1). 使用输入通道和输出通道相同的卷积操作；
2. G2). 谨慎使用分组卷积；
3. G3). 减少网络分支数；
4. G4). 减少element-wise操作。

通道分割在每个单元开始前将通道的输入分成两个，不再使用group卷积，然后concat两个channel并channel shuffle

轻量网络：squeezeNET

利用Fire module 来实现了：Link

Knowledge Distiall

实际上很简单，就是用小模型逼近大模型的输出，用大模型来做小模型的监督，也就是让小模型尽量去适应大模型的输出分布（原本应该只是一个类别标签），这其实已经偏向于一个无监督的驯良过程了，或者说是自监督。

• 训练大模型
• 计算大模型的soft output
• 训练小模型，在类别的监督信息以外再加上soft target的loss，用lambda来调节传中
• 使用小模型进行预测。

超参数搜索的方法

网格搜索，随机搜索，贝叶斯优化方法（这种方法实际上还不是太清楚，后面可能还需要看看），AutoML

激活函数的稀疏性

1. 适应性强，针对不同的情况有不同的激活单元
2. 简洁的模型，计算更快
3. 更好的预测能力和更不容易过拟合
4. 更可分

梯度消失与爆炸

消失：sigmoid ，tanh，

误差的反向传播造作，我们可以看出这种连乘的形式涉及到了很多的参数和导数，这种时候无论是放大还是缩小的效应都很容易累加起来产生梯度的消失或者膨胀，

当对当前层的w进行求导的时候，我们需要先对上一层的x求导，就会得到wt+1 与梯度连乘这样的式子，这也是导致梯度爆炸的原因

sigmoid的最大输出只有1/4所以sigmoid中梯度消失实际上是更常见的时候

再RNN中BPTT这种反向传播的时候也是类似的思路，但是它是以一个n维矩阵的方式向后传播的，这样当雅可比矩阵的特征值小于1的时候，这样的梯度传播会呈现指数级的变化，要么梯度消失要么梯度爆炸

ResNet 缓解深层网络中梯度消失的问题，实际并不是真正的解决这样的问题，只是给出了一个传播的shortcut，所以掩盖了梯度消失的情况出现，实际上ResNet解决更多的是模型退化的问题，也就是

梯度爆炸也可以使用梯度裁剪的方法进行解决：当梯度的范数大于阈值的时候，我们对梯度进行等比的搜索，

损失函数的反向推导

常见的几个损失函数和误差之间的关系（推一下grad的公式）

• Softmax
• CE

过拟合欠拟合的判断和处理方式

过拟合的训练方法：

• 获取更多数据

• 降低模型的复杂度

• 正则化方法：实际上这就是权重衰减的方法这里药剂的L1（直接减少有效参数的数量），L2正则化结构风险（减少权值过大带来的过拟合的风险）的那些具体定义；dropout等等。

  drop可以理解成bagging的办法的继承实现

• 集成学习方法，通过多个模型的集成来降低单一模型的过拟合风险

• early-stop

DROPOUT rescale

使用 pretraining 方法也可以帮助 dropout 训练参数，在使用 dropout 时，要将所有参数都乘以 $ 1/p$

• 开始时随机删除，一半P的神经元
• 在剩下的一般中更新，
• recycle，然后，最后学出来的参数的存在概率只有（1-P)所以要*概率。

欠拟合降低的方法：

• 添加新特征：特征与标签之间的相关性太差，我们可能需要挖掘新的特征；
• 增加模型的复杂度：简单模型的学习能力可能太差了，比如在线性模型中添加高次项，增加网络的深度或者神经元个数
• 减少正则化参数

有监督学习中涉及到的损失函数

LINKLINE

• 0，1损失函数： $max{0,1-fy}$ ,标签，二分类问题
• hinge损失（0，1的进化）：max{0,1-fy}

卷积

卷积的矩阵加速：https://www.mobibrw.com/2019/17787

转置卷积：LInk1 ；LInk2

转置卷积上采样带来的棋盘效应：https://www.cnblogs.com/hellcat/p/9707204.html

空洞卷积也会带来棋盘效应，也就是采样不均匀，有些点被重复采样，有些点没有被采样到，这样就会像棋盘一样，两种颜色分离的这种情况。

上采样 下采样：

SVD：https://www.cnblogs.com/endlesscoding/p/10033527.html

正则化的具体函数和内在含义

KEYPOINT：https://www.cnblogs.com/alexanderkun/p/6922428.html

实际上我们可以发现这也是一个权重衰减的操作，如果从导数去分析的话，或者我们数形结合，我们会发现这样的w和我们的函数曲线的交点实际上是偏向

Regularization：在目标函数中添加惩罚项，对复杂度高的模型进行惩罚，于是考虑从W的向量出发，

• 0范数：非零元素的个数，在机器学习中是个NP完全问题，很难求

• 1范数：绝对值之和

• 2范数，通常意义上的模，实际上从分布上来看

  L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的正则项||W||2最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别的哦；所以大家比起1范数，更钟爱2范数。

Normalization

重要参考资料 ；参考资料2向东的回答

权重伸缩不变性，可以有效的提高反向传播的效率，也有参数正则化的效果；

数据伸缩不变性；减少梯度弥散，简化对学习率的选择

covariate shift

协方差偏移，实际上是训练集和测试集中，变量的分布的不同带来的问题，这样就会导致模型的效果收到影响，也会印象网络的迭代速度，通过BN就可以将每个mini-batch的数据都拉回到标准正态分布，把带有偏差的数据拉回标准分布，拉回模型擅长的领域中，使得梯度变大，避免梯度小时的问题出现，也能加快收敛的速度。

帮助理解covariate shift ，更确切的来说，实际上是source domain和Target domain的数据分布不一致，他们的条件概率相同，但是边缘概率不同：

• 这样会导致不再是独立同分布：

• 需要不断适应输入的分布，降低学习速度

• 下端的变化可能趋向于变大或者变小，容易使得上层落入饱和区，学习过早的停止

• 会相互影响。

BN，IN，LN，WN

Normalization的基本框架就是 $h=f(g·\frac{x-\mu}{\sigma} + b)$

再次进行平移和缩放是为了模型的表达能力不因规范化而下降；这两个缩放因子是可以学习的，用来对底层的学习结果有所价值，这也会将数据变换到基本在非饱和区中（线性区），然后通过再次的缩放和偏移，提供了非线性。

BNnormalization纵向

是对同一个batch的所有图的逐channel进行的

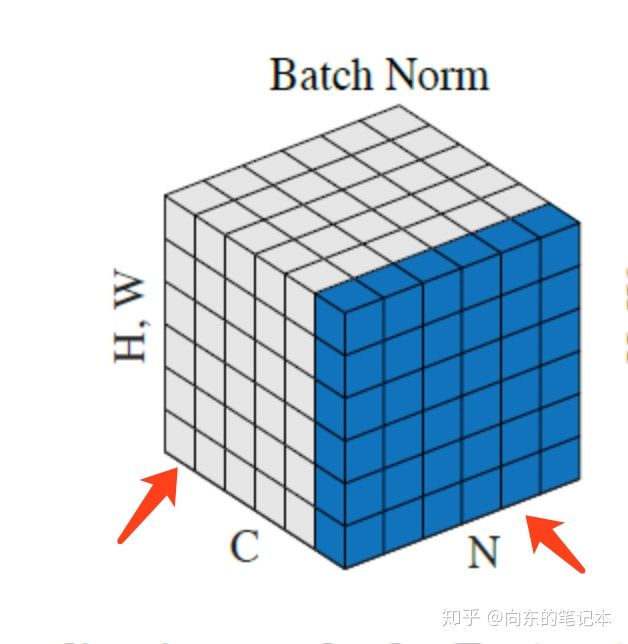
使用mini-batch来计算相关的均值和方差，element-wised；但是BN是独立的对每个维度（channel）进行统计的，这样的话，如果原始分布差距很大的话，会导致不同的数据训练，这样可能会增加模型的训练难度。

适用场景：每个mini-batch比较大，数据分布比较接近，所以我们需要进行充分的shuffle，不然效果会差很多。再运行中需要统计一阶和二阶统计量，所以不适用动态的网络架构和RNN，；相应的改造就不说了

适用于判别模型中，

Instance Normalization

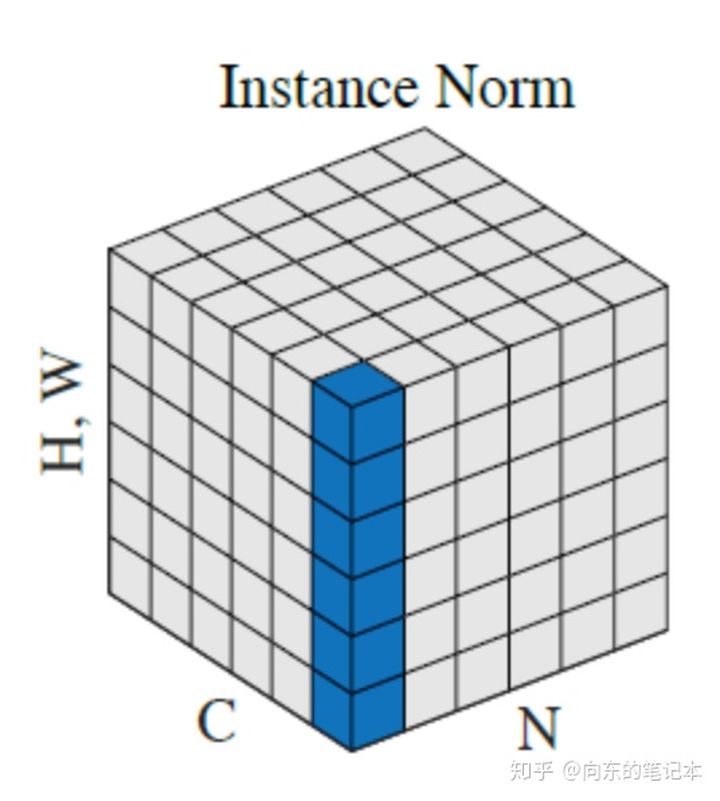
是对单张图片的单个通道单独进行的Normalization，适用于生成模型中，比如风格迁移，主要依赖的是单张图片的实例，所以不适宜对整个batch进行归一化，这样可以加速模型收敛和保证实例之间的独立性

Group Normalization

实际上就是一个normalization的变体：

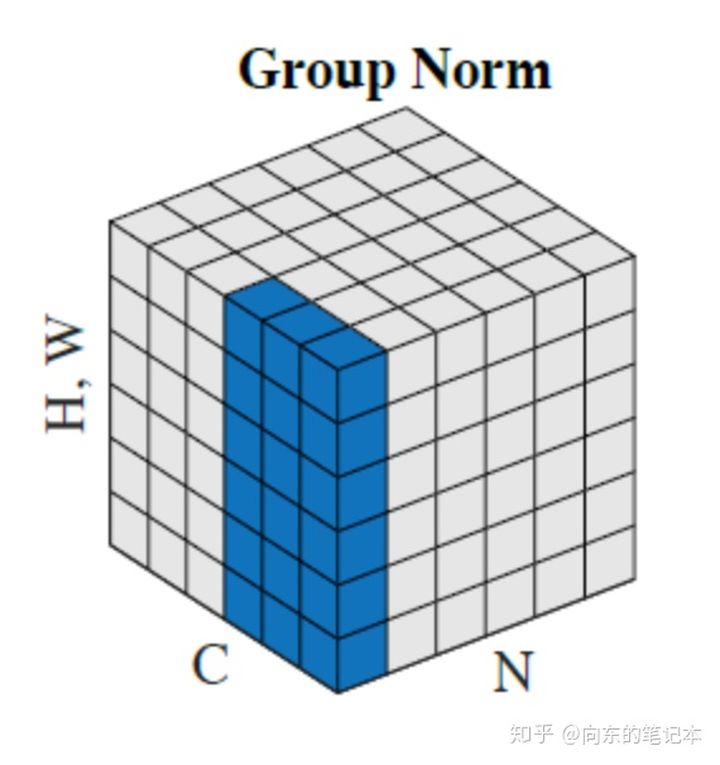
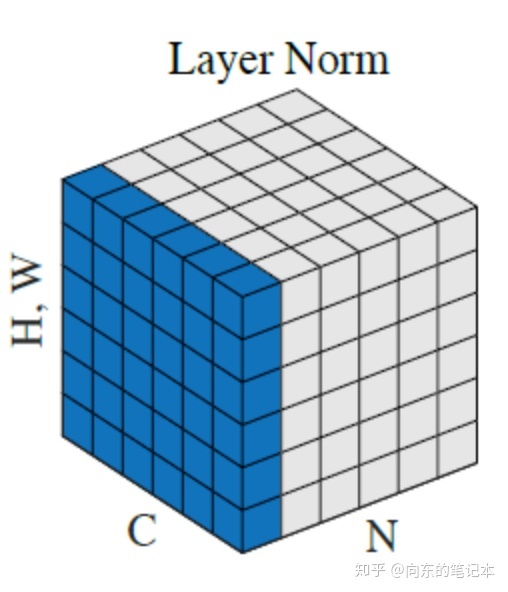
Layer Normalization 横向

是指对同一张图片的同一层的所有通道进行的normalization，所以和公式不一样的就是不需要求M的均值了，是对同一张图片的所有channel进行的

Wegiht Normalization参数规范化

CosineNormalization

解释一下attention

在某种程度上，注意力是由我么如何关注视觉图像的不同区域或者我们如何关联同一个句子中的不同单词所启发的：针对于问题的不同，我们会对图像的某些具体的区域重视（某些区域在视觉中呈现高分辨率，而另一些则是低分辨率的情况），或者句子中的某些词重视的情况。

比如我们看到eating就对food有更高的attention，与此同时color的权重就会比较低。

因为传统的RNN架构，固定的context vector可能会导致序列信息的缺失，可能无法记住长句子和时序对齐的信息，所以诞生了attention.

content vector和 attention weight加权，然后和上一个时刻的target和y，生成现在的y。

self-attention：https://zhuanlan.zhihu.com/p/47282410；

内部注意力，也就是内部的自我关联的获取，QKV的关系

Transformer 的基本架构

Transformer 的 Multi-Head 实际上就是有不同的QKV表示，然后我们将其表示起来。

mask屏蔽未来的信息

Pooling的反向传播：

Pooling层的主要作用

1、特征不变性，使模型更加关注是否存在某些特征而不是特征具体的位置，对于一些旋转和平移具有不变性
2、特征降维，使模型可以抽取更广泛围的特征，减小了下一层输入大小，进而减小计算量和参数个数

3、在一定程度防止过拟合，更方便优化

4、扩大感受野

avg pooling：均分后回传

MaxPooling：只传给最大的一项，其他项的反向传播值为0

Anchor-based和 Anchor-free的理解和辨析

实际上就是把五百问的内容再巩固一下，然后整理过来，这里还有两个比较相关的链接，到时候还不清楚就可以看下。

https://www.zhihu.com/question/356551927/answer/926659692

https://zhuanlan.zhihu.com/p/62372897

Anchor-based方法：在选练之前在训练集熵使用K-Means等聚类方法聚类出一组矩形框，代表主要的长宽，然后在推理时用这些Anchor滑动提取proposal之后在对这些Anchor进行回归和分类，比如扩张和中心点预测

Anchor-free:就是没有预先定义这样的BoundingBox，直接通过网络来预测相应的边框，比如左上角右下角，中心点这样的预测；中心点+长宽

机器学习部分

回归任务为什么难以训练

• 目标更难，需要适应所有的点
• 损失函数的角度，MSE之类的，下降与Value相关，对Outline敏感

Selective Search HOG SIFT

HOG: 手机知乎

Selective Search：https://zhuanlan.zhihu.com/p/27467369

SIFT：概览 ； 开贴细说

LR怎么处理低维线性不可分问题

特征工程或者使用多项式核和高斯核，将样本映射到可分的空间去进行逻辑回归；

线性回归和逻辑回归的异同点

实际上都是一个函数映射的问题，就是离散化和连续化的区别而已，还有其中的损失函数的设计等等

线性回归和逻辑回归实际上都是线性模型，但是最终一个映射到连续域做拟合，另一个映射到离散域做分类，最主要的区别就在于目的，输出值域，以及损失函数的设计上。

本质上都是一个一个线性映射函数的选择。

LR对连续值特征是怎么处理的

离散化的作用和优势：https://notes.001.io/lian-xu-te-zheng-li-san-hua/

LR本质上属于广义线性模型，通过进行值域的划分，相当于引入了非线性，从而提升了模型的表达能力；

进行离散化后对异常值不敏感，能对轻微的扰动有一定的鲁棒性，但是这还是比较考验特征划分技术的

可以对离散的特征值进行组合，进一步引入非线性

相当于简化了逻辑回归的模型，引入模型复杂度的正则化，这样能够减少过拟合的风险。

LR为什么要归一化

LR的求解过程不就是是梯度下降的方式，那么就是归一化的作用了没什么好说的

集成学习方法

Boosting

基学习器，做错的样本受到更多的关注，然后调整后的样本分布进行下一个基学习器的训练（AdaBoost）

对特定的数据分布进行学习，实际上就像是re-weighting的这样的操作；如果不能使用这种方法的模型我们就使用re-sampling的操作来处理。

• 过程中如果不满足比随机猜测好，这种模型就直接停止
• 可以看出这种方法主要关注降低偏差，可以对弱学习器构建出很强的集成

Bagging与随机森林

又放回的随机抽取样本构建包含m个的数据集，采样出T个这样的数据集，然后对这些基学习器进行结合，（简单投票做分类，简单平均做回归）

随机森林是在以决策树为基础构建的基学习器，在bagging的基础上，引入了随机的属性选择（原本是选择最优的），也就是先选择一个随机的子集，然后在子集中选择最优的用来划分。

GBDT和XGBoost

GBDT实际上就是BOOSTing的一种方法

都是通过损失函数相对于模型的负梯度方向来对当前的模型进行更新，但是在梯度下降里，我们的模型是通过参数表示的，而在梯度提升，是在函数空间中直接表示的。

通俗一点的说的话，实际上就是梯度下降是在更新梯度来进行梯度下降，梯度提升通过累加弱学习器来梯度下降。

关键：实际上在梯度提升中，梯度最终会被计算为（当作）残差，也就是用损失函数的负梯度去模拟残差

参考链接，里面也有提到区别 ；简单的实例分析

GBDT：Gradient Boosting Descend Tree

GBDT分类和回归时的基学习器都是CART分类回归LINK 树，每轮迭代在上一个基学习器结果的残差至上进行训练，（弱分类器）；

这里的残差可以更改为损失函数，然后最后还是会变成对残差的一个拟合，模型的残差实际上也不是这么好弄的，用损失函数的负梯度，来拟合本轮损失的近似值。然后就是从上到下一个个基学习器过去

不同的损失函数针对的是不同的问题（分类回归）

• 分类问题：指数损失函数和对数损失函数
• 回归问题：均方差损失函数，绝对值损失函数

GBDT的正则化：

• 给每个模型乘上一个弱化系数，降低每个模型对拟合损失的贡献
• 通过按比例来随机抽取样本训练模型，bagging，减少方差但是会增加偏差，可以使用交叉验证
• 控制CART的复杂度，可以使用剪枝正则化

优缺点：

• 灵活，准确率高，使用健壮的损失函数可以处理异常值
• 难以并行化处理，受限于基学习器之间的依赖关系

XGBoost

详细讲解XGBoost ；

和残差然后用CART拟合不同，我们是通过SCORE来确定结构，然后通过梯度的值来计算结构中应该有的值， 所以在我们计算完二阶梯度的时候，我们能同步的进行划分和复制，这样，但是还有为为什么要排序后去做，我有点没搞明白

两种方法的区别：

• 正则化防止过拟合，提升泛化能力 L1+L2
• 还可以使用线性分类器
• 使用了二阶导数信息来进行对代价函数的优化
• 采用和随机森林类似的策略，能对数据进行采样，降低过拟合和减少计算
• 有缩减项，类似weight decay
• 能计算出缺失值的分裂方向
• 可并行计算
• 划分的方式改成了一个Score（根据两阶段梯度数据）

SVM细节

在SVM推导部分的后面添加最终的形式以及整理一下KKT条件，通过这些特性对一些问题进行分析

为什么将原问题转化成对偶问题

1. 对偶问题将原始问题中的不等式约束转为了对偶问题中的等式约束
2. 方便核函数的引入,输入最终会转化从恒一种内积的形式
3. 改变了问题的复杂度。由求特征向量w转化为求比例系数a，在原始问题下，求解的复杂度与样本的维度有关，即w的维度。在对偶问题下，只与样本数量有关。

怎么转化到多分类的场景

不是逐个二分吗？

hinge损失的多分类形式：https://www.turingtopia.com/article/details/e2492b497a144bf6b3cd1fc62df60bbd

Lagrange乘数法，对偶问题

二次型函数 A是实对称矩阵

在 $R^N$ 上是凸函数和A是半正定矩阵是充要的关系；

凸规划：目标函数是凸函数，约束空间是凸集

MP是凸规划的条件：满足。。。

为什么凸规划是重要的，因为凸规划的任意局部最优值都是他的整体最优解

凸优化问题Lagrange：

• 引入松弛变量/kkt乘子，将不等式约束转化为等式约束，
• 引入拉格朗日乘子将等式约束转为无约束优化

KKT条件：MP（非线性规划）问题，可微可行点 $x^*$ 是整体最有解的条件 实际上是在凸规划的最优值求解过程中，使用拉格朗日乘数法，其中的不等式约束（<=0）需要满足的条件，其中：

求解Largrange，KT条件的时候我们通常使用互补松紧条件入手来求解（分情况讨论，但是这种时候要考虑分类的完备性来进行求解。）

对偶条件的引出

在线性规划的过程中可以使用对偶问题来进行转化，将求最大转化为求最小值；如果LP问题又最优解，则对偶问题也有最优解，且解相同

SVM的具体推导以及核函数

再生希尔伯特空间，

于是我们可以选择多项式核，高斯核，拉普拉斯核之类的来做这个核函数映射

核函数的记忆

相关的面试问题

SVM和LR的联系与区别：

• 他们都是分类算法，都是监督学习的模型

• 都是判别模型，如果不考虑核函数的话，都是线性分类算法

• LR采用log损失，SVM采用合页（hinge）损失

• LR基于概率理论，使用sigmoid和MLE来估计出参数的值；SVM基于几何的边界最大化原理

• LR对异常值敏感，SVM不

• 对海量数据来说LR效率高，在低纬度的时候LR的准确率高，但是维度上升就被反超

• 处理线性不可分：LR靠特征构造（组合交叉特征，特征离散化），SVM 还可以核函数

• LR是经验风险最小化，SVM自带结构风险最小化（自带了L2正则项所以）

将数据向SVM求得的超平面进行投影后，是否仍然线性可分？（数学推导，这里的推导我放弃）

显然不，从支持向量的角度分析，最优的结论必然是两点的中垂线，那么这种情况本身并不是线性可分的，但是如果超平面不是这个中出现的话，那么就不满足SVM求解条件中的最优分界面了。

70页开始，但是我决定先推导SVM，这一部分的内容再说吧

是否一定存在一组参数使得SVM的训练误差为0？

训练误差为0的SVM分类器一定存在吗？

加入松弛变量的SVM训练误差可以为0吗？

决策树

• 3种分支计算的方法：信息增益，增益率，gini指数

• 预剪枝，后剪枝

• 是否会重复利用连续值或者离散值特征来分树？

  离散特征不行，比如用西瓜的纹理来说：就是有没有了

  连续特征可以，阈值切割，我们可以不断的往下细分，比如<100 <50这样。

PCA与LDA

优化的目标：最大化投影方差， 在主轴上的投影方差最大，包含更多的信息量（信噪比的概念）。

通过这个思想去设计一个求解过程：中心化（为了使得投影后均值为0），然后求方差，然后推导出最大化问题，然后通过largrange乘数法，推出实际上就是特征值。

LDA投影到的是便于分类的，PCA是方差最大信息量最大的去除冗余的信息维度；无监督有监督

Boosting与Bagging

bagging 解决的是过拟合，boosting解决的是欠拟合的方法

这里需要重新再去温习一下基本的定义

MAP、MLE、Bayesian

https://blog.csdn.net/u011508640/article/details/72815981/

https://zhuanlan.zhihu.com/p/61593112

从数学意义上和模型上区分

显然基于bayesian公式我们可以区分后验和先验，以及使用贝叶斯公式去获得估计的基本依据是啥。（要看清楚似然的主体是啥，也就是求解的参数是那个）

这里的P实际上可以看成一个概率分布模型，一个推断模型（其中的D和θ一个是模型的数据一个是模型的参数）

前两者将

那么MLE（极大似然）：（频率学派，假设为定制）

我们把模型参数设置成θ（变量）然后，我们计算当θ等于多少的时候出现D这个数据的概率最大，（这样的话也就会引出我们对大量数据的需求，实际上是一个概率估计模型）

而MAP（最大后验概率）（和👇一样是贝叶斯学派，θ是随机数）

是贝叶斯估计的一种近似

也就是我们考虑了参数发生或者出现的先验概率以后再进行计算，由于上式的分母P(D)是个确定的值，所以不影响最大化的过程，我们通常再计算的时候将其忽略，然后最大化分子，就是MAP了，在这里这一步的prior是非常重要的，和我们之后的模型估计息息相关。

最后Bayesian估计

其中MAP估计的是后验的最大值，而贝叶斯估计是去近似这个后验函数，基于贝叶斯公式去做这个估计。（去看看数据挖掘中的这部分的题目来帮助理解）

朴素贝叶斯问题

看看数据挖掘中的那个讲稿，就很清楚，实际上就是类关系条件独立假设；

可以使用laplace校准来避免0概率对决策造成影响

那什么是朴素贝叶斯学习呢？

交叉熵 KL散度 信息熵

https://blog.csdn.net/b1055077005/article/details/100152102

无监督方法

K均值聚类的有优缺点：

• 受离群值影响，通常是局部最优解，类别量级和密度的问题没法解决
• 需要人工确定k
• 样本只能被划分到单一的类中

如何调优：

• 数据归一化，离群点处理
• 合理选择K值
• 核函数

证明K means 收敛：和EM算法实际上是一个框架，这里看一下关系

GMM：高斯混合模型

假定不同簇种的样本各自符合不同的高斯分布，这种得到的聚类算法就是高斯混合模型；

核心思想是：每个单独的分模型都是标准高斯模型，我们需要估计高斯分布的双参数，还有一个额外参数（权重或者生成数据的概率），实际上和K均值聚类是一样的操作过程，这里要记得EM。

使用极大似然（很难求解）去寻找均值方差和权重，所以最后使用EM去做

• 随机初始化参数，
• E：根据当前参数，计算每个点由某个分模型生成的概率
• M：根据概率，来改进每个分模型的均值方差和权重

SOM：自组织映射神经网络

nah

聚类算法的评估：

轮廓系数；霍普金斯统计量；R方

数据清洗

没用到就不说了，在数据挖掘中主要是：缺失数据，错误数据，和噪声数据

错误数据：分析更改删除和忽略

缺失数据：忽略，手工，填充（全局常量，属性或者中位数，基于贝叶斯等等方法（这个不提））

噪声数据：分箱（均值平滑，中值平滑，边界平滑），聚类，回归，人工检查

图像增强策略

torchvision.transformers的库里面有很多，还有unbalance_image中有一些经典的unbalance_image的一些策略

还有PIL中的Image.Enhance(这里可能要注意图像维度的转换)

1、对比度：白色画面(最亮时)下的亮度除以黑色画面(最暗时)下的亮度；

2、色彩饱和度：：彩度除以明度，指色彩的鲜艳程度，也称色彩的纯度；

3、色调：向负方向调节会显现红色，正方向调节则增加黄色。适合对肤色对象进行微调；

4、锐度：是反映图像平面清晰度和图像边缘锐利程度的一个指标。

MixUp的操作实际上就不要在赘述了，而Sharpen的操作实际上就是对分子分母都做一个1/T的乘方的这样一个锐化的操作，突出显著的样例，这样能够使得：？（需要加强记忆）

评估模块

ROC、PR、F1

PR曲线就比较清楚是根据Precision和recall区划分的，然后根据判定为正负样本的阈值去区分这个曲线的情况。

ROC曲线是根据 TPR和FPR真阳性率（正样本中有多少被判定为真）和伪阳性率（负样本中有多少被判定为真），依据score的阈值来绘制曲线

AUC越大，说明分类器越可能把真正的正样本放在前面

还有F1，是综合反应一个排序模型的性能(调和平均值)：

ROC比起PR来说，对于正负样本数据量的分布比较不敏感，所以在这种数据不均衡的大数据场景，ROC更合适，更广泛。如果是针对特定数据集上的表现的话实际上PR曲线的话能更直观的反应性能

RMSE

离群点可能导致效果一直很差，可以用归一化的百分比来看

余弦相似度

实际上就是将问题从距离转换到了角度上，用1-cos(A,B)表示余弦距离，实际上这种距离比起欧氏距离来说，能够适应更高的维度，比较相对差异的时候我们可以考虑用余弦相似度来衡量

不满足三角不等式：等腰直角三角形

在机器学习领域，还有kl距离，相对熵，也能衡量两个分布之间的距离，但是也不满足对称性和三角不等式

训练集和测试集的划分机制

• K次交叉验证法；

  首先描述一下什么是k次交叉验证，k次交叉验证的作用是：评估模型的预测性能，训练好的模型再新数据上的表现，在一定程度上减少过拟合，从有限数据中获取尽可能多的有效信息，使得模型对于数据的划分不那么敏感

• Handout检验：实际上就是7：3的随机划分的方式；其中还有留一划分的策略；

• 自助法（bootstrap）：有放回的随机抽样，总数为n的集合，抽样n次作为训练集，剩下的没有被抽样出来的数据作为测试集，这就是自助法的验证过程

  • 当抽样次数趋向于无穷的时候，有多少数据没有被选择过， $(1-\frac{1}{n})^n$ 取极限，根据重要极限 $(1+\frac{1}{n})^n$ 的极限是e，可以推得大概是1/e的概率没被选中，也就是大概百分之36%， （59页）

语言部分

Python部分

深拷贝浅拷贝

概念上是一致的，但是具体实现深拷贝上，是不一样的，python 应该是自带的.copy函数

https://www.jianshu.com/p/a71c09798123 )

修饰符的作用

修饰符的作用python函数修饰符@的作用是为现有函数增加额外的功能，常用于插入日志、性能测试、事务处理等等。

实际上就是讲函数作为作为输入参数，然后对函数进行包装，在执行函数之前或者之后增加一些操作，通常用来指示函数执行进程，也可以用来添加数据预处理等等

LINK REFERENCE

def log(func):
    def wrapper():
        print('log开始 ...')
        func()
        print('log结束 ...')
    return wrapper
    
@log
def test():
    print('test ..')

test()

多线程处理

一些基本的概念：

每个独立的线程有一个程序运行的入口、顺序执行序列和程序的出口。但是线程不能够独立执行，必须依存在应用程序中，由应用程序提供多个线程执行控制。

每个线程都有他自己的一组CPU寄存器，称为线程的上下文，该上下文反映了线程上次运行该线程的CPU寄存器的状态。

指令指针和堆栈指针寄存器是线程上下文中两个最重要的寄存器，线程总是在进程得到上下文中运行的，这些地址都用于标志拥有线程的进程地址空间中的内存。

• 线程可以被抢占（中断）。
• 在其他线程正在运行时，线程可以暂时搁置（也称为睡眠） – 这就是线程的退让。

使用threading作为线程处理模块：

run start join([timr])：等待至线程终止；isAlive() getName() setName()

append():添加到线程列表，使用for i in threads: i.join() 来等待所有线程完成。

1. 首先通过继承threading.thread创建子类，实现run操作；
2. 实例化之后使用start启动进程；

线程同步（Lock）

Lock和Rlock 都有相应acquire和release，

防止多个线程同时对某个数据进行修改，就需要对多个线程进行同步；

Python 中多线程和多进程的区别

这一点还是需要补充，好像是使用什么来着

主要从进程和线程本身的区别来谈，然后Python中的多线程是收到了Cpython的GIL约束的，所以稍微有点鸡肋，可能还是要用多进程去了解

[参考链接](

文件IO部分

文件处理：

读取键盘输入：a = input('请输入：')；

打开和关闭文件：open()，一般需要按照指定的格式打开一个文件才能对其进行修改或者读取。

fo = open("foo.ext","w")
fo.close()
# 相应的文件的读写实际上应该是
fo.write("dadsad")
res = fo.read(10)
# 使用tell 和seek输出和定位当前的文件位置，
# 实际上经常和with命令一起使用
with open(path,"w",encoding='utf-8') as f :
    # record the dir name (depth=1) 
    f.writelines(authorres)
    # record all the video
    for element in result:
        f.write(element)

补充说明： 这里with语句的解析

OS命令

chmod，chdir，chown，mkdir，path（一系列常用操作，exist之类的），getcwd（返回当前工作区），listdir（返回文件夹包含的文件或者文件夹的列表）

C++部分

实际上c++对于编写的顺序是有上下关系的，如果我们定义的时候遇到了一些上面和下面的差别的时候，我们可以考虑在上面先进行declaration，在后面在具体的进行definition。

文件操作：

基本读写

写文件步骤如下：

1. 包含头文件 #include <fstream\>

2. 创建流对象 ofstream ofs;

3. 打开文件ofs.open("文件路径",打开方式);

4. 写数据ofs << "写入的数据";

5. 关闭文件ofs.close();

读文件的操作步骤如下

1. 包含头文件 #include <fstream>

2. 创建流对象 ifstream ifs;

3. 打开文件并判断文件是否打开成功 ifs.open(“文件路径”,打开方式);

4. 读数据 四种方式读取

5. 关闭文件 ifs.close();

处理二进制文件

二进制方式写文件主要利用流对象调用成员函数write

函数原型 ：ostream& write(const char * buffer,int len);

参数解释：字符指针buffer指向内存中一段存储空间。len是读写的字节数

打开方式要指定为 ios::binary；

二进制方式读文件主要利用流对象调用成员函数read

函数原型：istream& read(char *buffer,int len);

参数解释：字符指针buffer指向内存中一段存储空间。len是读写的字节数

预编译头

首先介绍的是如何防止在重复的include<head.h>的时候,不会导致重复的定义和include的方式，以及其中的区别

#pragma once：自定义包含了这种情况的时候，依赖于不会将同一个文件多次编译，这个方式没办法保证内容相同的不同名文件被重复的编译，针对的是文件。

#ifndef ：依赖于宏名称不能冲突，这个能保证内容相同的不同文件不小心被同时包含，实际上是一个预编译的条件语句

首先介绍一下写法：

基本的逻辑也就是当我们第一次执行的时候，就会预先定义到这一块，这样到时候就不会导致相应部分的代码被重复的执行或者定义
#ifndef _code_block
#define _code_block
// code here
#endif

在自己编写的时候需要注意不能重复使用宏名（_code_block），不然可能会出现以外的其他地方的代码没有被执行。

多线程

mutex互斥锁

内存分区模型

主要将内存分为四个区域:

• 代码区：存放函数的二进制代码，由操作系统进行管理

  程序运行前进行分配

  存放CPU执行的机器指令，具体而言代码区是共享的和只读的

• 全局区：存放全局变量、静态变量和常量

  这部分空间应该是在预编译的时候事先分配的

  该部分的数据再程序结束后由操作系统释放

• 栈区：由编译器制动分配和释放，存放函数的参数值，局部变量等

• 堆区：由程序员分配和释放，如果程序员不释放，程序结束后由操作系统回收；

（类内的存储特点）：

在c++中，类内的成员变量和成员函数分开存储，只有非静态的成员变量才属于类的对象上的存储。（函数也是不占对象空间的，所有的函数共享一个函数实例）

（static）静态成员函数在编译阶段分配内存，类内声明类外初始化，所有的对象共享同一份数据；

类：

THIS指针

指向的是，当前调用的这个 对象；

友元friend：

通过friend关键词告诉编译器其他的可以访问类中私有内容的东西；

友元可以是：

• 函数
• 类
• 其他类别的成员函数

继承

构造函数顺序

继承的时候首先调用父类的构造函数，在构造子类的构造函数，析构是反向的。

几种继承方式

注意区分继承方式面临的主体，也就是说：

• 派生类能访问的元素实际上都是除了私有类都能访问
• 区别在于我们是否能通过派生类的实例对基类的变量进行访问，这里的继承方式就代表着这些变量在被继承之后的状态，是私有的保护的，还是公共的

父子的成员同名

无论是不是静态，都是：

• 访问子类同名成员 直接访问即可
• 访问父类同名成员 需要加作用域

多态

多态是C++面向对象三大特性之一

多态分为两类

• 静态多态: 函数重载 和 运算符重载属于静态多态，复用函数名
• 动态多态: 派生类和虚函数实现运行时多态

静态多态和动态多态区别：

• 静态多态的函数地址早绑定 - 编译阶段确定函数地址
• 动态多态的函数地址晚绑定 - 运行阶段确定函数地址

多态使用时，如果子类中有属性开辟到堆区，那么父类指针在释放时无法调用到子类的析构代码

解决方式：将父类中的析构函数改为虚析构或者纯虚析构

​ 1. 虚析构或纯虚析构就是用来解决通过父类指针释放子类对象

​ 2. 如果子类中没有堆区数据，可以不写为虚析构或纯虚析构

3. 拥有纯虚析构函数的类也属于抽象类

常用STL函数

• for_each：遍历容器
• transform：搬运容器中的数据到另一个容器中
• accumulate：计算容器的元素综合
• fill：向容器中添加元素
• replace_if
• find_if
• set_union：求两个容器的并集
• set_intersection：求两个容器的交集

通用部分：

深拷贝和浅拷贝的概念：

浅拷贝：简单的赋值拷贝操作

深拷贝：在堆区重新申请空间，进行拷贝操作

同步与异步