@AikenHong 2021 @Code: Scipy(repo) @Reference: 匈牙利算法&KM算法
该篇笔记用来介绍匈牙利算法和KM算法(Kuhn-Munkres Algorithm),这两个算法通常用来做目标之间的匹配问题。 常用于:多目标跟踪,和深度聚类中的标签匹配问题。
Method
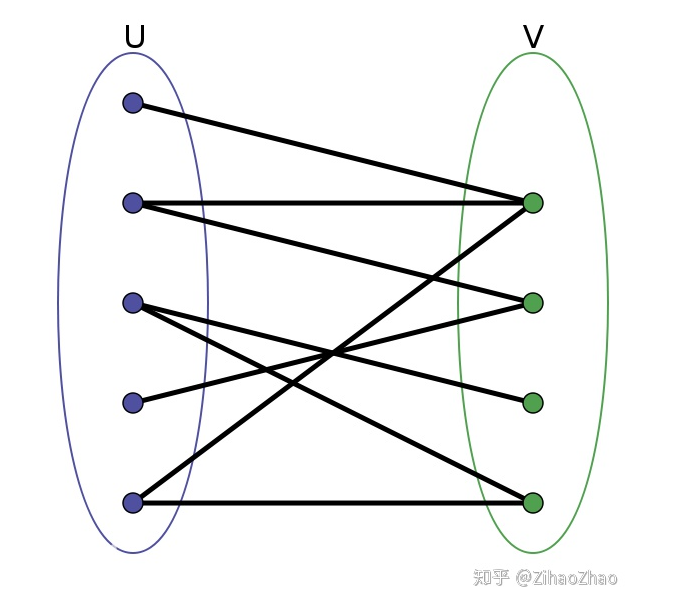
这两种方法实际上解决的问题都是: 二分图的最大匹配问题; 首先需要对二分图有个基本的了解:
实际上就是将数据分为两组,各组的每一个点都去另一个组找对应的匹配,我们希望将两组中,相关的数据尽可能的准确的匹配起来。
可以想象成,是同一个数据在不同的映射下的不同表征需要做这样的匹配关系。
解决这种问题的方式就是使用匈牙利算法或者KM算法
匈牙利算法
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法
匈牙利算法可以将二分图中的连线,看成是我们认为可能是相同的目标(不带权值),实际上就是从上到下假想成立,然后进行唯一匹配的搜索,有点像BackTrack的过程。
整体算法的成功率或者准确率实际上十分依赖与连线的准确率,对算法输出预测的准确度要求更高。
KM
KM解决的是带权的二分图的最优匹配的问题。
相当于我们给每条线都给出一个置信度预测值,基于这样的权值图去计算对应的匹配关系
Step1: 将左边节点标上与他所关联的最大权值的边的数值 Step2: 寻找匹配,原则如下
- 只有权重和左边分数相同的边才进行匹配;
- 如果找不到边,此条路径的所有左边顶点-d,右侧+d,这里我们将d取值为0.1
- 对于考虑换边的另一个节点,如果无法换边,也需要对应的进行-d
具体的例子可以这么看(最好还是看blog):
Code
使用scipy中的集成版本实现,但是要注意对应的输入是二分图的cost_matrix
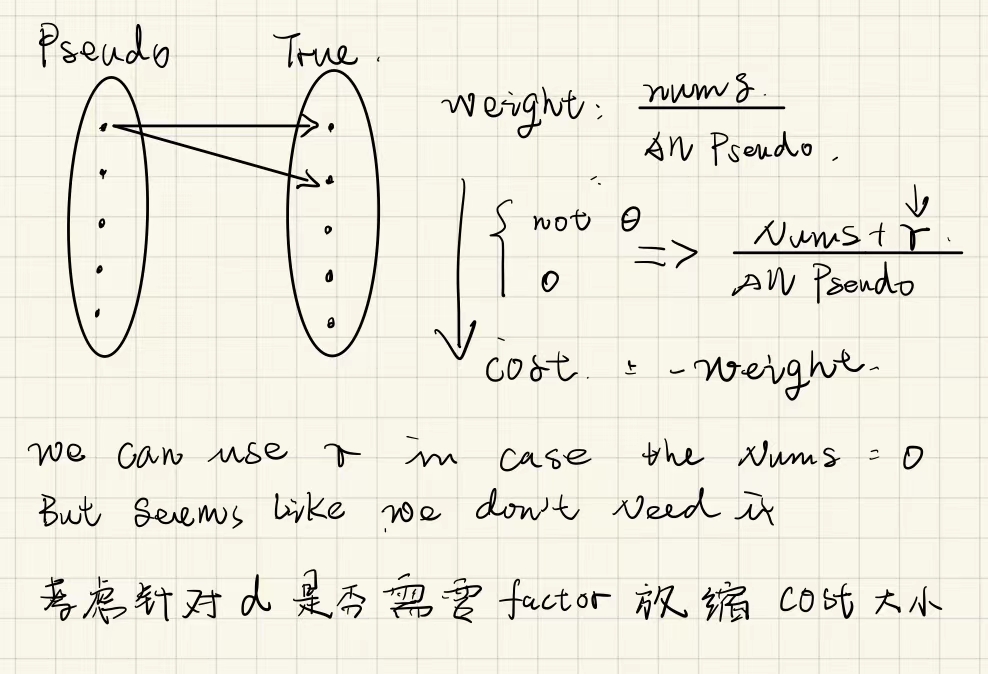
算法的实现应该是将最大的权值转换成了最大代价来进行计算的,所以为了使用KM算法,我们首先应该构造对应的损失矩阵。
假如我们使用相似度指标计算的话,对应的大小关系应该做一个反转,可以直接用负号进行计算,计算完相似度直接取一个负值进行计算。
from scipy.optimize import linear_sum_assignment
row_ind, ol_ind = linear_sum_assignment(cost_matrix, maximize)