fGAN 对GAN理论的深度理解

@Aiken 2021 onenote部分的拓展编写，到时候拷过去，整合在一起。

fGAN: 不只是JS-Div散度，我们可以将所有的散度都应用到GANs的框架中。该部分的阅读是对GAN的基本理论最重要的文章之一。

基本理论体系和推演

首先给出fGAN中提出的基本理论：可以将所有的Div放入GANs的框架中，来做那个核心的关键演化判别指标：

$$ D_{f}(P||Q) = \int_xq(x)f(\frac{p(x)}{q(x)}dx) $$

上述公式将衡量P和Q两个分布之间的差距，公式中的 $f$ 可以是很多不同的版本，但是要求满足如下的两个条件：

是一个凸函数； $f(\frac{(x1+x2)}{2})\leq \frac{[f(x1)+f(x2)]}{2}$ ，需要注意国内外的凹凸相反
$f(1)=0$ 。

而我们知道 $q(x)$ 是概率密度分布函数，实际上可以看成凸函数性质的推广，所以我们可以证得：

$$ D_{f}(P||Q) = \int_xq(x)f(\frac{p(x)}{q(x)}dx) \geq f(\int q(x) \frac{p(x)}{q(x)} dx) = f(1) = 0 $$

显然当我们取得合适的f，KL（ $f(x) = xlog(x)$ ）; ReverseKL( $-log(x)$ )；chi square ( $f(x) = (x-1)^2$ )；

Fenchel Conjugate共轭

补充Fenchel共轭的知识来对后续的fGAN推导进行补充，定理内容如下：

每个凸函数都有一个对应的共轭函数读作 $f^*(x)$

$$ f^*(x) = \max \limits_{x\in dom(f)} xt - f(x) $$

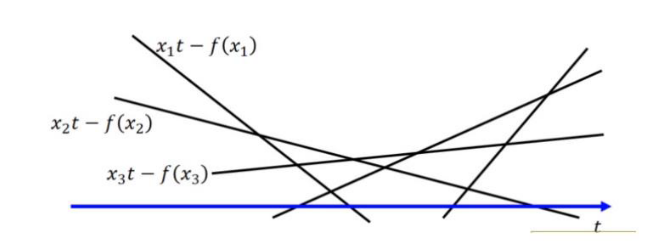
t是给定的，对于所有的变量t， $xt-f(x)$ 对应了无数条直线：

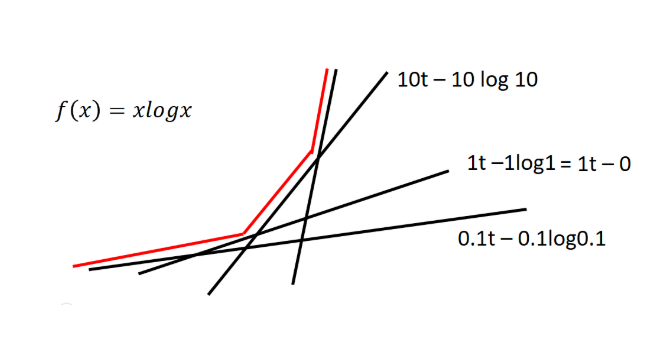
举个例子 $f(x)=xlog(x)$ 时，我们可以将对应的 $f^*(x)$ 画出来。

实际上就是对给定的t，求 $g(x)$ 共轭方程的最大值的过程，求个导，然后就可解得 $x->t$ 然后带回就能得到共轭方程。

介绍共轭方程主要是为了和 $f(x)$ 进行转化

$$ f^{*}(t)=\sup _{x \in \operatorname{dom}(f)}\{x t-f(x)\} \quad \Leftrightarrow \quad f(x)=\max _{t \in \operatorname{dom}\left(f^{*}\right)}\left\{x t-f^{*}(t)\right\} $$

F-Div GAN推导

将转化方程带入，利用简单的不等式转化，我们就能将之前的F-Div转换为一个类似GAN的式子：

$$ \begin{aligned} D_{f}(P \| Q) &=\int_{x} q(x) f\left(\frac{p(x)}{q(x)}\right) d x \\ &=\int_{x} q(x)\left(\max _{t \in \operatorname{dom}\left(f^{*}\right)}\left\{\frac{p(x)}{q(x)} t-f^{*}(t)\right\}\right) d x \\ & \geqslant \int_{x} q(x)\left(\frac{p(x)}{q(x)} D(x)-f^{*}(D(x))\right) d x \\ &=\int_{x} p(x) D(x) d x-\int_{x} q(x) f^{*}(D(x)) d x \\ & \approx \max _{D} \int_{x} p(x) D(x) d x-\int_{x} q(x) f^{*}(D(x)) d x \end{aligned} $$

解释一下：第三行就是由于t是随便取值的；最后一行就是我们要求一个D使得式子最大，上界实际上就是第二行的式子。

这样我们就能推导出F-Div的变体：

$$ \begin{aligned} D_{f}(P \| Q) & \approx \max _{D} \int_{x} p(x) D(x) d x-\int_{x} q(x) f^{*}(D(x)) d x \\ &=\max _{D}\left\{E_{x \sim P}[D(x)]-E_{x \sim Q}\left[f^{*}(D(x))\right]\right\} \end{aligned} $$

对于生成器来说，我们就是要找到一个PG使得：

$$ \begin{aligned} G^{*} &=\arg \min _{G} D_{f}\left(P_{\text {data }} \| P_{G}\right) \\ &=\arg \min _{G} \max _{D}\left\{E_{x \sim P_{\text {data }}}[D(x)]-E_{x \sim P_{G}}\left[f^{*}(D(x))\right]\right\} \\ &=\arg \min _{G} \max _{D} V(G, D) \end{aligned} $$

这样我们的推导过程就结束了，然后我们也可以使用更多的Div Function，使用不同的Div距离直接选择对应的函数就可以了。

JS Div不是最佳的Div

由于分布的数据之间是没有重合的，使用JS Div的时候就很难衡量出他的距离，Equally Bad

为什么如果两个分布完全没有重合的话，那么这两个分布的 JS Div 会是一样的?
前面有提到，JS Div 是通过判别器计算出来的，而判别器的本质是二分类器，只要 $P_G$ 与 $P_{data}$ 完全没有重合，判别器就能 100%地鉴别出 $P_G(x)$ 与 $P_{data}(x)$ 的差异，因此二者的 JS Div 就是一样的。

LSGAN最小二乘

解决的就是没有重合的问题，解决思路如下：让判别器始终都不能100%的鉴别出差异，这样就能保证在没有重合的时候也能分辨出差异程度。

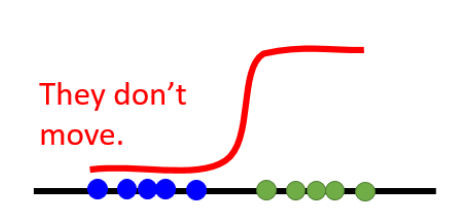
当我们的D太好的时候（能将数据完全分开）这种时候生成器就优化不了了，也是Equal Bad带来的最大问题。那么如果我们将最终的激活从sigmoid换成linear激活层，这样训练出来的D就会是一个线性的直线，

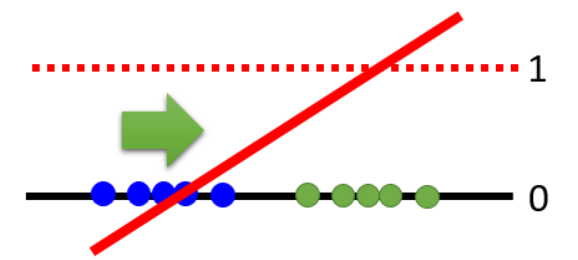
这样只有当完全重合的时候D才会是一个没有梯度的直线，但是这个也并没有真正的解决这个问题，而只是绕开了这个问题。

真正解决了这个核心问题的是下面的WGAN

Wasserstein-GAN

核心思想：用Wasserstrin距离（EM距离）取代JS距离

fGAN 对GAN理论的深度理解#

基本理论体系和推演#

Fenchel Conjugate共轭#

F-Div GAN推导#

JS Div不是最佳的Div#

LSGAN最小二乘#

Wasserstein-GAN#